本文节选整合自深度学习「花书」（Deep Learning, Ian Goodfellow et al.）第三部分的读书总结。花书可以在英文版网站或中文版翻译仓库上取得。

深度生成模型

判别模型与生成模型

深度学习乃至整个机器学习领域在有监督学习上取得了最大的成就。在有监督学习的过程中，每个样本 $x$ 由 $n$ 个特征组成，并被打上了 $m$ 维标签 $y$，从大量样本中可以学得一个条件概率分布 $p(y|x)$，我们将该分布称为一个判别模型。

但是更多的机器学习任务要求我们不仅能够进行分类和回归，而是对样本 $x$ 的性质获得一些知识，这样的任务包括生成样本、处理缺失值和去噪等。这些任务要求我们学习 $p(x)$ 本身（称为生成模型），由于 $x$ 的维度往往非常高，目前还没有通用的方法进行学习。

结构化生成模型

不妨设 $x$ 的每个特征都是一个离散随机变量并有 $k$ 个不同的取值，最简单暴力的方法是去参数化每一个组合的概率，这需要 $k^n-1$ 个参数才能完成。显然，这些参数数量巨大，无法高效完成概率计算和采样，而且容易导致过拟合。

事实上，如果每个特征各不相关，则 $p(x)$ 可以很容易地因子化为 $\prod_ip_i(x_i)$；但即使特征之间相关，相互作用往往局限于很少量的特征之间，我们需要一种更加精准的语言来描述这种关系。

一种策略是使用有向无环图，我们将每个变量用一个结点表示，然后把变量之间的依赖关系用有向边表示。具体来说，令 $\prod_ip_i(x_i|a(x_i))$ 其中 $a(x_i)$ 表示 $x_i$ 依赖的所有父结点。选取什么样的依赖关系，取决于我们对给定问题的先验知识，例如给定 $t=(t_0,t_1,t_2)^T$，如果我们认为 $t_2$ 不依赖于 $t_0$，则有 $p(t)=p(t_0)p(t_1|t_0)p(t_2|t_1)$, 对应的有向无环图是

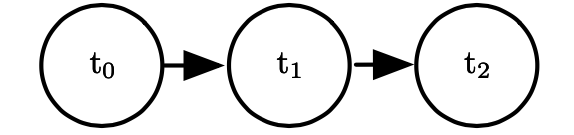
这种形式使得我们参数化或采样都变得比较容易。

但若我们不想为依赖关系指定明确的方向，则可以使用无向图。无向图中每个结点仍代表一个变量，我们为图中的每一个团（两两相连的结点子集）$C$ 指定一个概率因子 $\phi$，则（未归一化的）概率函数可以写作 $\tilde p(x)=\prod_C\varphi_C$。例如，上例改为无向图后，因子化表示为 $\tilde p(t)=\phi_1(t_0,t_1)\phi_1(t_1,t_2)$ 只要每个团中结点数不多，这个形式也比整体概率分布要容易参数化。

潜变量

即使使用图模型，各个变量之间的相互作用也可能非常复杂。但除了样本中的不同特征之外，我们也可以引入一些潜变量 $h$，如果在模型中 $x_i,x_j$ 都与 $h_k$ 有相互作用，那么模型也能描述 $x_i$ 和 $x_j$ 的相互作用；而 $p(x)$ 可以表示为 $p(x)=\int p(x,h)\mathrm dh$.

生成模型涉及的计算

配分函数

在无向图中，由于概率因子不是归一化的，我们通常只能知道未归一化的 $\tilde p$ 而不是 $p$，类比统计力学中的情况我们可以定义配分函数 $Z$：

如果该式不能解析求出，通常需要 Markov 链 Monte Carlo（MCMC）等方法进行近似计算。

边缘概率

如果 $p(x,h)$ 难以通过积分或求和求出边缘概率分布 $p(x)$，那么我们在利用对数似然函数进行梯度下降时 $\arg\max_\theta\sum_ip(x_i,\theta)$ 就会遇到问题。通常，我们试图找似然函数的一个下界，然后对这个可计算的下界进行优化来近似对似然函数的优化。

采样

如果图是有向无环的，那么我们可以按照图的拓扑排序采样；否则采样就将是比较困难的。除了继续使用 Markov 链之外，我们还可以考虑 Gibbs 采样（作为 Markov 链的一种特殊情况）。

在 Markov 链中，我们定义一个转移矩阵 $T(x'|x)$，不断对 $x\leftarrow x'$ 进行更新，从而使得它渐渐趋于原始分布。但一般来说构造转移矩阵 $T$ 比较困难。Gibbs 采样是 Markov 链的一种实现方案，设所有变量可以划分为 $A,B$ 两个集合，如果 $A$ 中的变量都确定下来后 $B$ 中所有变量是条件独立的，那么可以同时对 $B$ 中所有变量进行采样。这在具有二部图的结构中尤其有用。

以下我们讨论一系列常见的深度生成模型。

无向图生成模型

Boltzmann 机

我们将样本中的变量记作 $v$（可见变量），而将模型额外定义的隐变量记作 $h$，简单起见 $v$,$h$ 都是二值向量。则 Boltzmann 机给出的概率模型为

Boltzmann 机虽然形式非常简单（仅仅是一个多元正态分布），但由于潜变量的存在，对潜变量求完期望后可以得到任意复杂的 $p(v)$ 的形式，可以证明它可以以任何精度近似离散变量上的概率分布函数。

Boltzmann 机具有难以处理的配分函数，需要用上一节中提到的方法来近似；但或许更严重的问题是不容易进行边缘概率计算，这是因为 $v$ 和 $h$ 以复杂的方式纠缠着。基于此，我们可以提出一个受限 Boltzmann 机，它的函数形式是

可以看出它具有类似于下图的无向二部图结构：

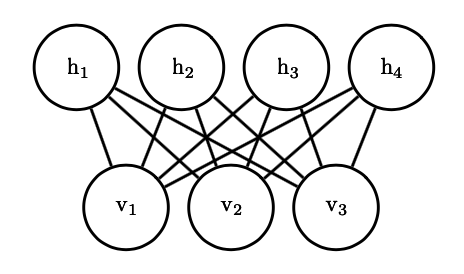
容易证明，如果我们对受限 Boltzmann 机进行 Gibbs 采样，每次固定可见变量不变时，隐变量的概率分布是因子化的，可以同时采样：

其中 $\sigma$ 是 Logistic 函数 $1/(1+e^{-z})$，而 $\odot$ 是两个向量的逐元乘积。类似地，$P(v|h)$ 也是因子化的，因此能够高效地进行 Gibbs 采样。

深度 Boltzmann 机

正如单个隐变量层的神经网络通常不如更深的神经网络高效一样，我们也可以向 Boltzmann 机上加入更多层隐变量来提高它的描述能力。下图给出了一个三层 Boltzmann 机的图示，注意到如果它仍然是受限的（同层不连接），它仍然具有二部图结构，与单层受限 Boltzmann 机一样容易计算条件概率。

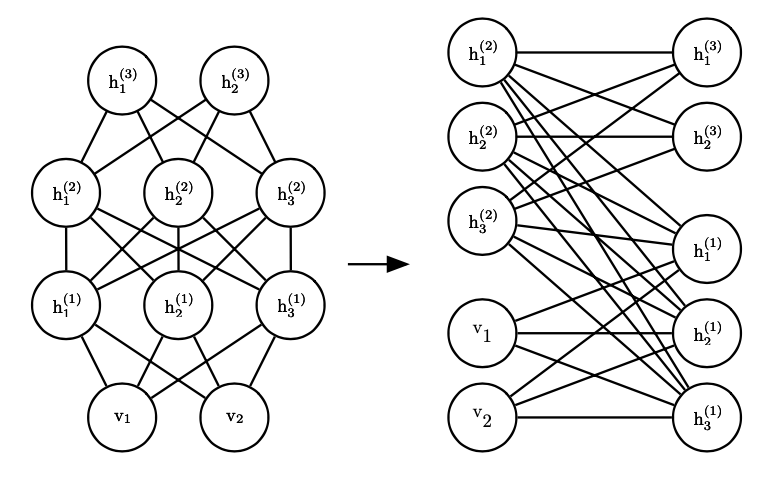
但是采样时，我们需要对所有层同时运行 MCMC，这通常比较困难。为了解决这个问题，出现了深度信念网络。深度信念网络在网络的最深处保留了一层无向图结构，但其余地方都使用有向图，这样我们对最深层进行 MCMC 采样后就可以依次迭代计算其余层的采样。

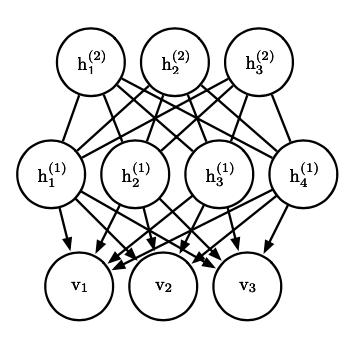
有向图生成模型

自回归网络

无论 $p(x)$ 多么复杂，一个朴素的想法是把它作如下分解： $p(x)=\prod_ip(x_i|x_1,\cdots,x_{i-1})$ 也即按变量下标的顺序逐级分解为条件概率，然后对条件概率进行参数化，这称为自回归网络。最简单的线性自回归网络可以用下图表示：

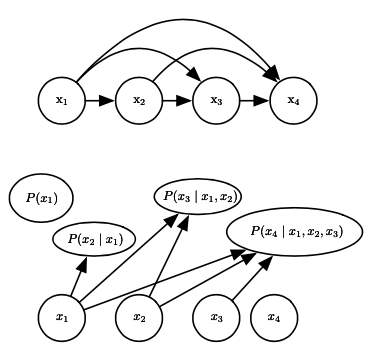
其中每个条件概率都由线性回归来描述。为了进一步增大自回归网络的容量，我们可以向其中加入隐变量，得到如下结构：

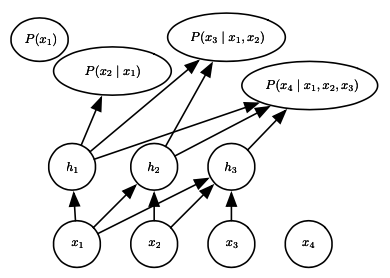
每个变量首先处理为隐变量，这一映射关系保持了「自回归」的特性不变，并且隐变量的层数可以任意增加，这被称为神经自回归网络。

生成器网络

我们可以首先从一个比较简单的分布 $p_z(z)$ 中采样，然后通过非线性函数 $x=g(z;θ)$ 得到 $x$ 的样本，然后通过调节函数中的参数来得到想要的 $p(x)$。具体来说，我们有

如果 $g$ 可逆，并且 Jacobi 行列式也容易计算，那么我们可以直接用最大似然来优化 $\theta$，这样我们就得到归一化流方法。

但对于更复杂的 $g$ 来说一般不是如此。为此我们需要找到其他方法来优化 $\theta$，这里我们仅以变分自编码器方法为例进行介绍。

由于 g 可以看成是一个解码器，我们考虑一个有噪声的编码器 $q(z|x)$，容易证明对于任何 $q$，以下泛函均小于 $p(x)$：

也即 $L(q)$ 是 $p(x)$ 的一个变分下界。由于 $q$ 是一个有噪编码器，我们可以把它参数化为 $q(z|x)=\mathscr N(z;\mu(x;\theta),\sigma^2(x;\theta))$，也即给定一个 $x$，某个待定的函数形式给出 $\mu$, $\sigma^2$，然后 $z$ 按上述多元正态分布；这两个函数可以分别用神经网络来训练。而泛函 $L(q)$ 不需要涉及边缘分布 $p(x)$，因此可以通过 Monte Carlo 采样来计算。

总结

深度生成模型无疑处于深度学习的前沿，其核心任务对 $p(x)$ 的建模需要我们针对具体的问题思考哪些变量可能存在相互作用，分析它潜在的概率图结构，然后选取相应的模型加以运用。