在经典和半经典的分子动力学中,我们经常会用到比较复杂的函数形式来描述系统的势能 ,这些势能进而可以在分子动力学模拟中用于力的计算。尽管力(作为势能的负梯度,)的表达式原则上可以机械化地由势能的表达式推出,在实际计算的时候我们经常需要手工计算梯度,然后将梯度的表达式再一次编码到程序中。
显然,这一方案并不足够优雅:面对复杂的势能表达式,手工求导容易出错,且由于求导出错导致的异常行为(例如,势能-力不一致使得系统能量不守恒)难以排查。在开发阶段,对势能进行调整时同时对力进行调整不是一个好的工作流,这对于力场开发者来说尤为明显。
数值求导与符号求导
一个自然的思路是数值求导,即利用中心差分
计算导数。中心差分的一个明显的问题是精度,毕竟差分仅仅是对微分的近似;误差通常与步长 h 呈 V 形曲线关系,即步长大时截断误差占主导,步长小时舍入误差占主导。如下图所示,程序设计者必须对体系有充分的了解,才能选择合适的步长:
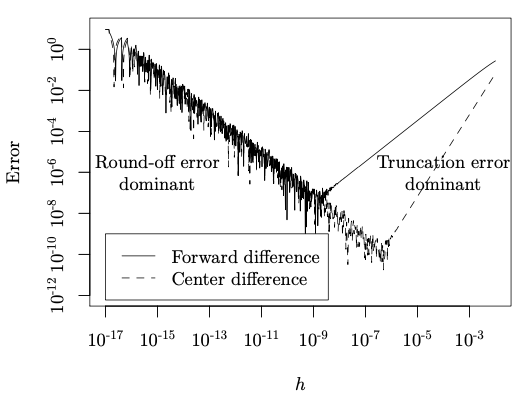
典型差分计算中误差与步长的关系
一个更明显的问题是计算量。若 是 维的,则获得梯度需要 2n 次函数求值,对于复杂的势函数来说显然是不可取的。
我们也可以考虑让程序进行符号求导,也即基于基本的导数运算规则推出导数的表达式,再代入表达式求值。这看起来不错,但在实际应用的时候常常陷入一种「表达式爆炸」的状况。我们考虑一个非常简单的情况,即某一函数是多个子函数的乘积:
这样一来,它的导数将包含 k 项,但绝大多数的项是相互重复的。这些项再分别进行自身的求导,最终会生成庞大的表达式,使求值效率很低。重复项可以通过合适的缓存技术消除,不过计算机的化简能力有限,不容易写出通用的缓存办法。
自动求导:前向与后向
「自动求导」看起来不是一个好的名字,因为它常常与或数值或符号的求导方法相混淆。使它区别于其他方式的核心理念在于:
使用导数的运算规则来找出求导的路径,但在路径上并不展开全部的表达式,而是立即计算数值,以此避免重复计算和「表达式爆炸」的情况。
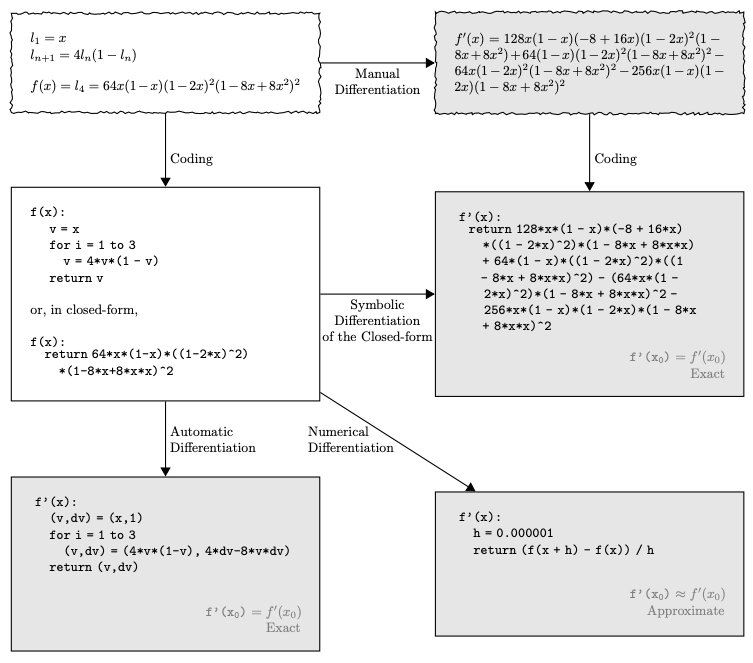
这张图很好地总结了四种不同求导方式之间的关系。
自动求导按其实现的思路,可以分为前向自动求导和后向自动求导。在此仅指出,对于梯度计算后项求导比较占优势,其时间复杂度一般认为仅比原函数大了一个固定的常数倍数,即
这里 c 根据具体系统不同而一般在 1~3 之间。
计算图、求值轨迹、伴随轨迹
为了实现后向求导,我们首先需要构建一张计算图(显然它是一个有向无环图)。考虑一个二元函数 我们可以将计算过程中所有的中间变量的依赖关系画在一张图上:
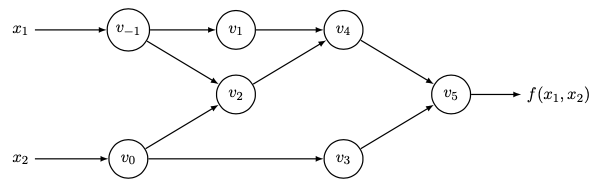
函数 的计算图
图中 ,,,,然后将它们求和即得到了 (也是最终的结果)。
给定输入数值,我们可以在图上正向迭代,得到一条求值轨迹并记录各个中间节点的数值。然后,对每个中间变量,我们都定义相应的伴随变量:
显然,,我们据此将图反向迭代,每个节点上的取值取决于有多少前方的节点依赖了它。例如传播到 时,发现这个节点只能通过 影响到 ,那么 就可以表示为
其中,前方的伴随变量 等都是已经算好的,而偏导数则是根据求导规则算出来的对其他节点数值的调用(这些数值在求值轨迹上已经求出来了),例如
最终我们将它反向迭代到输入变量处,就获得了导数。
自动求导的实现
根据计算图是什么时候构建的,可以将自动求导的实现方法分为两类:函数重载和源代码转换。
函数重载是将求导抽象为对图上节点的一种运算。不妨设 ,我们定义一种关于常规伴随变量的二元函数 ,则图在这一步的反向传播可以表示为 ,由此就可以在运算的过程中动态地反向迭代该图。
而源代码转换则是将反向迭代图的过程用该语言的源码直接表示出来并加以编译,运行过程中不涉及图的运算,但是实现过程中需要较多的编译器知识。因此一般来讲,函数重载比较易于实现,而源代码转换比较高效。
在 Julia 语言中,Zygote 是基于源代码转换的后向自动微分,而 ReverseDiff 则是基于函数重载的后向自动微分。我们接下来用 ReverseDiff 来实现一个简单的分子动力学程序。
辛可分经典系统的幂零子系统分解
在经典力学中,若记相点 ,则相点的运动方程可以很简洁地写成 ;由此我们也可以算出相点的二阶导数:
一般来说, 不恒等于 0;不过我们可以考虑一些使 的特殊的系统(幂零系统),在这些系统中 Taylor 展开式由于 而被截断到只有两项
因而在求解运动方程的时候可以简单地用向前欧拉法计算。显然如果哈密顿量只是动能或只是势能的函数,那么这个条件是满足的。
现在我们考虑一类辛可分系统,即哈密顿量可以写成 的形式,我们考虑如下分解
对应于每个子系统,它是幂零的,因此向前 Euler 算法引起的变换是辛的,因而它们相继变换也是辛的,并且通过合适地调整系数 能使这一算法具有任意高的精度。
我们首先定义一个系统:
using ReverseDiff
struct System
V::Function
T::Function
V_q::Function
T_p::Function
q::Vector
p::Vector
System(V, T, q, p) = begin
T_p(p) = ReverseDiff.gradient(T, p)
V_q(q) = ReverseDiff.gradient(V, q)
new(V, T, V_q, T_p, q, p)
end
end
然后定义一个算法,它包含了我们刚才提到的系数数组:
struct Integrator
a::Vector
b::Vector
end
一般来说由于时间反演对称的要求,a 的大小会比 b 多一个。所以我们把演化算法这么写(重载函数调用):
(integrator!::Integrator)(system::System, dt::Real) = begin
for i in 1:length(integrator!.b)
system.p .-= integrator!.a[i] * system.V_q(system.q) * dt
system.q .+= integrator!.b[i] * system.T_p(system.p) * dt
end
system.p .-= integrator!.a[end] * system.V_q(system.q) * dt
end
现在假设我们写好了自己的势能和动能函数,嗯,就叫它们 awesomePotential 和 awesomeKinetic 吧,皮一下:
awesomePotential(q) = sum(x -> .5x^2, q)
awesomeKinetic(p) = sum(x -> .5x^2, p)
system = System(awesomePotential, awesomeKinetic, rand(2), rand(2))
最简单的分解是二阶 Verlet 算法
对应于系统的演化是
所以我们构建一个这样的方法,然后运行:
integrator = Integrator([.5, .5], [1])
for _ in 1:1e5
integrator(system, .1)
end
总结
从一个「道」的层面上来看,科学计算中各项新理念的提出不仅是一种技术的提高,更推动了一部分工作方式的变革,使我们更少地关注实现细节,实现对物理概念的更高层次抽象,从而更深刻地认识所研究的内容。
前几天看了冰冰写的《物理、数学和 CS 中的 Global 与 Local》,感觉很有趣,如果全局性和局域性(大致可对应到 Isaiah Berlin 提出的刺猬思考者与狐狸思考者)反映了思维方式的基本差异的话,我更偏向全局性,愿意欣赏优雅的、具有形式美的东西,并将某种更大的希望寄寓其中。
你对自动求导怎么看?打算怎么用?欢迎你在留言区与大家分享。